Jiez19971225‘s Blog

做自己爱做的事

0%

左偏树

发表于 更新于 分类于   |   字数统计: 992(字)   |   阅读时长: 4(分)

最后一篇以前写的文章了，

左偏树是一种实现简单的可并堆，可以在 logn 的复杂度下面完成优先队列的插入，删除，合并操作。

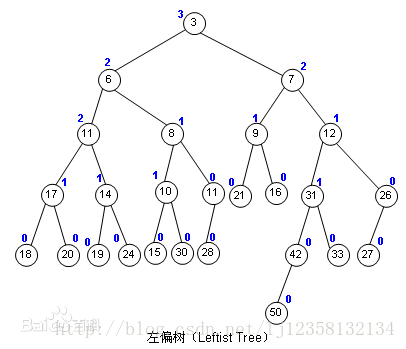
这就是一颗左偏树啦 蓝色是该节点的 dist

左偏树

结构体定义

1
2
3
4
5
6
struct Node{
    int l,r,d,v;//左右子树，距离和键值
    Node(){
        l=r=v=d=0;
    }
}

我们定义左偏树的外界点为，一个左子树为空或者一个右子树为空的结点，结点的 dist 为它到它子树内外节点的最短距离。一个左偏树在满足堆的性质的前提下还应该满足它的右子树的 dist 不大于它的左子树的 dist。由此，我们可以得出其他一些性质。

当前结点的 dist 为右子树 dist 的长度+1
若左偏树根节点的 dist 为一定值，则节点数最少的左偏树是一颗完全二叉树，并且为满二叉树
由上一条性质，可以知道根节点 dist 为 n 的左偏树，最少含有 2n+1−12n+1−1 个结点
一个有 n 个结点的左偏树，根节点距离最大为|log2（n+1）|−1|log2（n+1）|−1
左偏树的操作（最大堆）

递归合并
如果有一颗树为空，返回另一棵树
否则，就将根节点键值较大树的右子树和根节点键值较小树合并
如果合并后破坏了左偏树的性质（左子树 dist<右子树 dist）
交换根节点的左右子树
更新根节点的 dist 值

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
int merge(int x,int y){
    if(!x){
        return y;
    }
    if(!y){
        return x;
    }
    if(node[x].v<node[y].v){
        swap(x,y);
    }
    node[x].r=merge(node[x].r,y);
    if(node[node[x].l].d<node[node[x].r].d){
        swap(node[x].l,node[x].r);
    }
    node[x].d=node[node[x].r].d+1;
    return x;
}

插入
相当于和只有一个结点的树合并

1
2
3
4
5
int insert(int x,int v){
    cnt++;
    node[cnt].v=v;
    return merge(x,cnt);//返回新的根节点
}

堆操作

1
2
3
4
5
6
int top(int x){
    return node[x].v;
}
int pop(int x){
    return merge(node[x].l,node[x].r);//返回新的根节点
}

以上操作都以左偏树堆顶的编号代表这一刻左偏树
例题 hdu1512 左偏树加并查集的模版题，今年省赛的热身赛就是这题来着，当时乱搞搞出来了（数据太弱），重新用左偏树写一下。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
#include<iostream>
#include<cstring>
using namespace std;
const int maxn=1e5+7;
int cnt=0;
int n,m;
int p[maxn],pqroot[maxn];
struct Node{
    int l,r,d,v;
    Node(){
        l=r=v=d=0;
    }
    void fight(){
        l=r=d=0;
        v/=2;
    }
}node[maxn];
int merge(int x,int y){
    if(!x){
        return y;
    }
    if(!y){
        return x;
    }
    if(node[x].v<node[y].v){
        swap(x,y);
    }
    node[x].r=merge(node[x].r,y);
    if(node[node[x].l].d<node[node[x].r].d){
        swap(node[x].l,node[x].r);
    }
    node[x].d=node[node[x].r].d+1;
    return x;
}
int pop(int x){
    return merge(node[x].l,node[x].r);
}
int find(int x){
    return x==p[x]?x:x=find(p[x]);
}
int uset(int x,int y,int root){
    p[x]=y;
    pqroot[y]=root;
}
int main(){
    //freopen("in.txt","r",stdin);
    while(cin>>n){
        memset(node,0,sizeof(node));
        memset(p,0,sizeof(p));
        memset(pqroot,0,sizeof(pqroot));
        node[0].d=-1;
        for(int i=1;i<=n;i++){
            p[i]=i;
            pqroot[i]=i;
            scanf("%d",&node[i].v);
        }
        cin>>m;
        for(int i=0;i<m;i++){
            int p1,p2;
            scanf("%d%d",&p1,&p2);
            int s1=find(p1),s2=find(p2);
            if(s1!=s2){
                int pqroot1=pqroot[s1],pqroot2=pqroot[s2];
                int newroot1=pop(pqroot1);
                int newroot2=pop(pqroot2);
                node[pqroot1].fight();
                node[pqroot2].fight();
                newroot1=merge(newroot1,pqroot1);
                newroot2=merge(newroot2,pqroot2);
                int newpqroot=merge(newroot1,newroot2);
                uset(s1,s2,newpqroot);
                printf("%d\n",node[newpqroot].v);
            }else{
                printf("-1\n");
            }
        }
    }
}

并查集维护一个当前集合内优先队列的根节点 pqroot，合并的时候注意根的相关操作就 OK 了。