kmp算法

推荐 B 站一个 UP 的视频，讲的非常容易理解 链接

暴力匹配思路

设模式串为 sp，要匹配的目标字符串为 st

扫一遍 st，每次从 st 当前位置开始匹配 sp，这样做浪费了大量时间，之前匹配过程得到信息没有被有效利用。

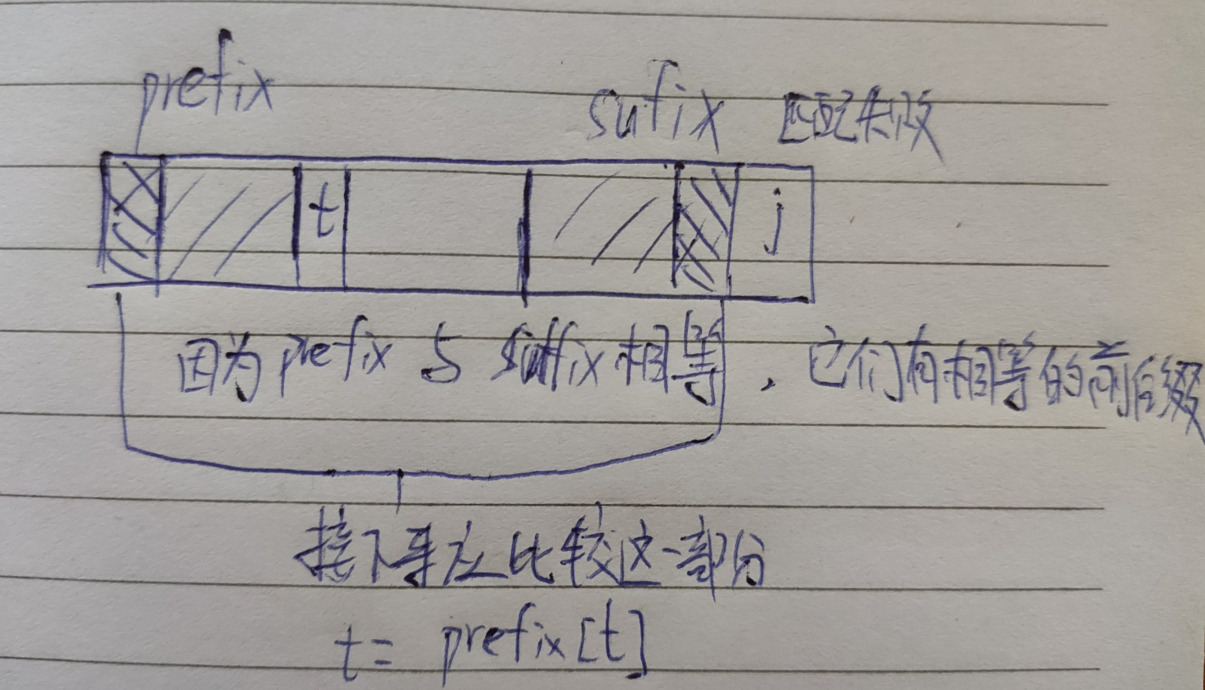
KMP 算法

最大公共前后缀

KMP 中为了有效利用之前已获得的信息，使用了最大公共前后缀。
前后缀的概念我们都知道，而公共前后缀是指该位置的前缀与后缀相同的部分。应当注意，前缀是不能包含当前位置的，而后缀不能包含第 1 个位置。
举个例子，ABCDABC 中，C 位置的最大公共前后缀是 ABC。
我们计算 AAAAB 的最大公共前后缀，使用 presuf 数组保存最大公共前后缀的长度
则 presuf = [0,1,2,3,0]

KMP 算法流程

构造最大前后缀数组

首先构造 presuf 数组，构造的流程如下

为了方便算法编写，令 presuf[0] = -1 作为边界，最大公共前后缀从 1 下标开始记录。
令 j 表示当前指针位置，可以理解为后缀指针，t 表示前缀指针位置。

t = presuf[0] = -1
m = sp.length()
while j < m-1
    // 当前位置前后缀匹配，更新 presuf 数组
    if t < 0 || sp[j] == sp[t]
        presuf[++j] = ++ t
    // 当前不匹配，则应该缩小前缀的范围
    else
        t = presuf[t];

匹配流程

i = 0
j = 0
m = st.length()
while j < m
    if i < 0 || sp[i] == st[i]
        ++i,++j
        if i == sp.length()
            // 得到结果
    else
        // 这一步也很好理解，和构造过程是一样
        i = presuf[i]

代码实现

为了便于理解，变量名都是用了更具意义的缩写

#include <bits/stdc++.h>
using namespace std;
const int maxn = 10005;
int main()
{
    string st = "AAAAAAAAB";
    string sp = "AAAAB";
    int presuf[maxn];
    memset(presuf, 0, sizeof(presuf));
    // 构造过程
    int prep = presuf[0] = -1;
    int sufp = 0;
    while (sufp < sp.size())
    {
        if (prep < 0 || sp[prep] == sp[sufp])
        {
            presuf[++sufp] = ++prep;
        }
        else
        {
            prep = presuf[prep];
        }
    }
    // 匹配过程
    int stp = 0, spp = 0;
    int res = -1;
    while (stp < st.size())
    {
        if (spp < 0 || st[stp] == sp[spp])
        {
            ++spp, ++stp;
            if (spp == sp.length())
            {
                res = stp;
                break;
            }
        }
        else
        {
            spp = presuf[spp];
        }
    }
    cout << res;
}

应用

KMP 算法的应用，判定一棵二叉树是否是另一颗二叉树的子树，如果这棵树的序列化字符串是另一棵树序列化字符串的子串，则可以判定。