有穷自动机

（以下内容摘自龙书）

有穷自动机是一般化的状态转换图，它可以是确定的或不确定的，其中不确定的含义是，对于某个输入符号，在同一个状态上存在不止一种转换。

下文以 DFA 指代确定的有穷自动机，NFA 指代不确定的有穷自动机。

DFA 和 NFA 都能且仅能识别正规集，即它们能够识别正规表达式所表示的语言。DFA 导出的识别器比 NFA 导出的识别器快得多，但是 DFA 可能比与之等价的 NFA 大得多。

NFA

NFA 是由以下几个部分组成的数学模型：

一个状态的有穷集合 S
一个输入符合集合$\Sigma$,即输入符号字母表
一个转换函数 move，它把状态和符号组成的二元组映射到状态集合
状态 $s_0$ 是唯一的开始或初始状态
状态集合 F 是接受（或中止）状态集合

NFA 可以用带标记的有向图表示，称为转换图，其节点是状态，有标记的边是转化函数。

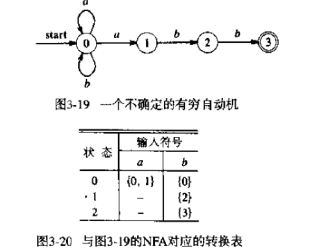
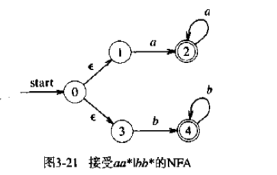
DFA

DFA 是 NFA 的特例

没有一个状态具有$\epsilon$转换
对每个状态 s 和输入符号 a，最多只有一条标记为 a 的边离开

确定的有穷自动机在任何状态下，对任一输入符号，最多只有一个转换。如果用转换表表示 DFA 的转换函数，那么表中的每个表项最多只有一个状态。因而，很容易确定 DFA 是否接受某输入字符串，因为从开始状态起，最多只有一条到达接受状态的路径可由这个符号串标记。

NFA 转为 DFA

子集构造算法，在 NFA 的转换表中，每个表项是一个状态集，在 DFA 的转化表中，每个表项只有一个状态。从 NFA 变换到 DFA 的基本思想是让 DFA 的每个状态对应 NFA 的一个状态集。DFA 用它的状态去记住 NFA 在读输入符号后到达的所有状态。

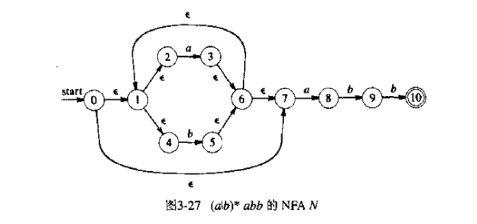
定义三种操作

$\epsilon-closure(s)$ 从 NFA 状态 s 只经过$\epsilon$转换可以到达的 NFA 状态集
$\epsilon-closure(T)$ 从 T 中的状态只经过$\epsilon$转换可以到达的 NFA 状态集
move(T,a) 从 T 中的状态 S 经过输入符号 a 上的转换可以到达的 NFA 状态集

子集构造的步骤伪码如下，其中 Dstates 是 D 的状态集合，Dtran 是 D 的转换表

初始时，$\epsilon-closure(s)$是 Dstates 中唯一的状态且未被标记

while Dstates 中存在一个未标记的状态T
    标记T
    for 每个输入符号a
        U = epsilon-closure(move(T,a))
        if U 不在 Dstates中
            将U作为一个未标记的状态添加到Dstates中
        Dtran[T,a] = U

开始状态 A = $\epsilon-closure(s)$ = {0，1，2，4，7}，根据算法流程，先标记 A

然后计算 $\epsilon-closure(move(A,a))$，在状态 A 上只有 2 和 7 有 a 上的转换，得到状态 B={1,2,3,4,6,7,8},Dtran[A,a] = B

状态 A 中只有状态 4 对于输入 b 有一个转换，得到状态 C={1,2,4,5,6,7},Dtran[A,b]=C

然后对没被标记的状态 B 和状态 C 继续这个过程

状态 B 的 a 转换得到的状态仍然是 B， Dtran[B,a] = B

状态 B 中在 8 上的 b 的转换可以得到新的状态 D={1,2,4,5,6,7,9} Dtran[B,b] = D。这里的计算详细解释一下，{1,2,3,4,6,7,8} 经过 b 转换后的集合是 {5,9}，然后再计算 $\epsilon-closure({5,8})$ 得到 {1,2,4,5,6,7,9}

状态 C 的 a 转换可以得到的状态 {1,2,3,4,6,7,8}，即状态 B，Dtran[C,a] = B

状态 C 的 b 转换可以得到的状态 {1,2,4,5,6,7}，即状态 C 自身，Dtran[C,b] = C

之后的过程省略，可以得到的五个状态集合是

A = {0,1,2,4,7}
B = {1,2,3,4,6,7,8}
C = {1,2,4,5,6,7}
D = {1,2,4,5,6,7,9}
E = {1,2,4,5,6,7,10}

状态	a	b
A	B	C
B	B	D
C	B	C
D	B	E
E	B	C

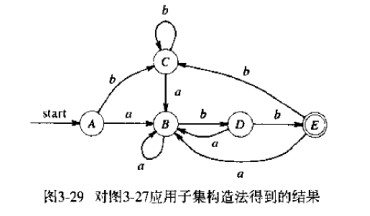
代码实现

接下来用编程语言实现一个简单的 DFA

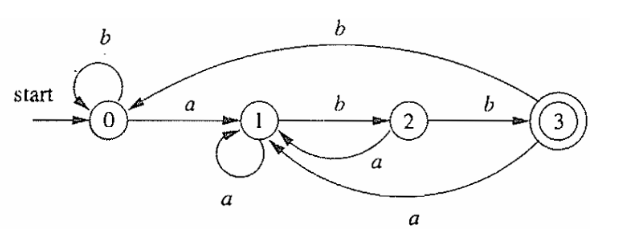
功能要求：输入一个单行无空格的字符串（以“#”号结束），如果该字符串是一个合法的输入，则显示“接受”，否则显示“不接受”。

分析该 DFA 的五元组信息如下

一个状态的有穷集合 S = {0,1,2,3}
一个输入符合集合$\Sigma$ = {a,b}
一个转换函数 move，它把状态和符号组成的二元组映射到状态集合
- move(0,a) = 1
- move(0,b) = 0
- move(1,a) = 1
- move(1,b) = 2
- move(2,a) = 1
- move(2,b) = 3
- move(3,a) = 1
- move(3,b) = 0
状态 $s_0$ 是唯一的开始或初始状态 = 0
状态集合 F 是接受（或中止）状态集合 = {3}

根据如下信息就可以开始编码了

#include <bits/stdc++.h>
using namespace std;
string str;
void dfa()
{
    bool ok = true; // 是否合法
    int pos = 0;    // 当前扫描位置
    int state = 0;  // 当前状态
    while (str[pos] != '#')
    {
        char next = str[pos];
        ++pos;
        if (state == 0)
        {
            if (next == 'a')
            {
                state = 1;
            }
            else if (next == 'b')
            {
                state = 0;
            }
            else
            {
                ok = false;
                break;
            }
        }
        else if (state == 1)
        {
            if (next == 'a')
            {
                state = 1;
            }
            else if (next == 'b')
            {
                state = 2;
            }
            else
            {
                ok = false;
                break;
            }
        }
        else if (state == 2)
        {
            if (next == 'a')
            {
                state = 1;
            }
            else if (next == 'b')
            {
                state = 3;
            }
            else
            {
                ok = false;
                break;
            }
        }
        else if (state == 3)
        {
            if (next == 'a')
            {
                state = 1;
            }
            else if (next == 'b')
            {
                state = 0;
            }
            else
            {
                ok = false;
                break;
            }
        }
    }
    if (state != 3)
    {
        ok = false;
    }
    if (ok)
    {
        cout << "接受" << endl;
    }
    else
    {
        cout << "不接受" << endl;
    }
}
int main()
{
    while (cin >> str)
    {
        dfa();
    }
}

输入：
abbab#
abb#
输出：
不接受
接受